Please understand that while they include references to scholarly papers, the following ideas represent interpretations of those articles by an amateur, and should not be considered in any way to be accepted viewpoints. Our ideas are presented as a framework, we understand that the actual math and physics when discovered will be exponentially more complex than what we describe. Yet we are convinced that the universe is fundamentally atemporal and aspatial, where energy determines the characteristics and relative position of matter. There is no fundamental space, no fundamental time, only emergent space and time generated by changes in relative position (sequential events explained by causal set theory).
"It seems more natural to regard the metric as a statistical property of discrete spacetime. Instead we want to suggest that the concept of absolute time ordering, or causal ordering of, space-time points, events, might serve as the one and only fundamental concept of a discrete space-time geometry. In this view space-time is nothing but the causal ordering of events." Myrheim J (1978) Statistical Geometry. Tech. Rep. CERN-TH-2538.
If your goal is to understand spacetime as science now believes it to be, then you should limit your reading to the Summary and Links above. If you want to venture into what would now be viewed by many as part science, part pseudo-science, part science fiction, and perhaps all wrong, then read on.
We believe that traditional interpretations of general relativity and quantum uncertainty are less than adequate. Note that we say "interpretations", not theories, we think that our ideas are compatible with both general relativity and quantum physics. We believe that there is no fundamental time or space. Space is derived from the relative position of observables and time is derived from any change in those relative positions. Visualize the entire universe as a stage with a couch, chair, and two actors. So long as the relative position of each object does not change there is no passage of time. If the positions of the actors change relative to the furniture we interpret that as motion through "space" and "time". Now think about removing the stage, the furniture and actors are floating in an empty universe. Here is the tricky part, how are we going to know if anything changes if we double the distance between all the objects? At first you may think it would be easy to tell, but remember in our normal world we have a background, a stage, to judge distances by. If there is no background we are convinced there is no time and no space. (While we don't think change would be detectable, we should note that even if everything scaled uniformly it might be possible to detect the changes by measuring gravitational waves, gravitational lensing, etc.)
We believe that experimental confirmation of quantum entanglement supports the idea that there is no spatial or temporal separation between objects, there is only relative position in an atemporal / aspatial universe. It seems impossible to explain instantaneous communication between entangled particles if there is fundamental space between them, but if there is positional but no spatial separation quantum entanglement is easily understood. If we are right we live in a universe where there is no past or future, where objects that exist exhibit relative positions that when changed (pre-symplectic mechanics) animate that existence. Objects that do not exist cannot be said to possess a past or future worldline, objects that do exist have a finite set of transitory relative positions. In some sense we are simultaneously living in a dynamically generated, temporary, past, present, and future. Objects that do not change relative position and do not experience time or space. The relative positions of every atom in our bodies constantly change, giving us the illusion of passage of time and movement through space. We will briefly explain what, beyond intuition, we base our conclusions on.
Special relativity is part of general relativity, and is valid only under a limited set of conditions. The theory of general relativity provides strict rules that neither special relativity, nor any of our other theories of the universe, can violate. The problem with space-time is that general relativity tells us that there is no fundamental "metric" that can be constructed on the space-time "manifold", there is just a manifold, or perhaps no manifold at all. A space-time "metric" is a distance function that has properties similar to distance in Euclidean space and that is used for relating a number to every pair of objects in space-time, somewhat like a grid on a map is used to calculate the distance from A to B. A space-time manifold is a topological space equipped with a family of local coordinate systems that are related to each other, containing every event that ever happens.
As we just said, a "world-line" is the history of an observer in "space-time". Space-time is essentially the history of the entire universe, containing every "event" that ever happens. Each point on the world-line is generally thought to be a real physical event at a unique point in space-time. Special relativity allows us to define a distance from the origin for all the points on a world-line, allowing the world-line to be a set of points that have physically distinguishable properties. Therefore, we can identify each of the events on a world-line as distinct points in space-time.
If our universe is in fact fully relativistic, with no fundamental metric, it is quite possible that in general relativity there is no sense in which we can talk about the "length" of a "world-line". It may be that we cannot even say that, given two manifolds, a world-line in one is a world-line in the other "plus an extra bit", simply because two such four dimensional manifolds with two "different" world-lines exhibit diffeomorphism invariance and represent the same physics. This would mean that the two world-lines in the two manifolds could not be distinguished from each other (similar to not being able to tell if our car is at rest or in motion). In other words, a manifold with one shape can undergo a diffeomorphic transformation into a manifold of another shape, and the laws of physics cannot be used to distinguish one from the other - you simply cannot tell which one you are in!
If this is a correct interpretation of general relativity, if we cannot construct a metric on the space-time manifold, it is possible that the points on a world-line cannot be thought of as representing something different from each other. It is quite possible that the only information that a particle's world-line contains is that the "particle exists". If so, there would be nothing about the world-line that describes something that exists in "time", and there would be no temporality of any kind associated with the world-line!
The best way to introduce our viewpoint is to ask the following question, "Assume that every object in the universe stops moving. If every object is frozen in space, does time continue to tick away?" The common sense answer is that it does. The best guess answer from quantum theorists, string theorists, and special relativity advocates is that in some sense it does. Yet the best guess from those who believe that general relativity should be taken literally, is that time stops when relative motion stops.
A few of the physicists who specifically study "space-time" go one step further and assert that general relativity does not tell us that time stops, rather Einstein's field equations tell us that on a fundamental level "time" does not exist at all! They argue persuasively that "time" is not a fundamental part of the universe, rather "time" is a quantity that is derived from the relative motion of objects in the structure we call "space" (which itself may or may not be fundamental). In a frozen universe there is no "time", only "space" (perhaps a different kind of space than we think it is, perhaps no space at all - only relative position). This is what we believe to be true.
The following example illustrates our ideas. Assume that the only objects in the universe are two rows of dominoes, row A and row B. Assume that both rows are frozen in space, no domino is moving relative to any other domino.
It is clear that in some sense "space" exists because the two rows are frozen in space. The "space" that the rows occupy appears to be quite real, even if it is just the relative "position" of the dominoes. Yet if in this universe we ask, "What time is it?", we cannot give an answer. There is no clock to measure time by, indeed there is no motion that we can use to define time. There appears to be nothing in the universe except the objects and the space that they occupy. We believe that time simply does not exist in this universe. Therefore space (relative position), and not time, is the fundamental observable quantity in this universe (as we said above, perhaps even space is not fundamental). Now assume that both rows start falling.

It is clear that we can calculate the "time" it takes for row A to fall by comparing it to the "rate" of fall of the dominoes in row B, just like we would do if we compared the falling dominoes to the motion of the second hand on a watch. It is also clear that we can calculate the "time" it takes for row B to fall by comparing it to the rate of fall of the dominoes in row A. For every one domino that falls in row A, two fall in row B. We can choose row A as our clock and, in a sense, row B as our "ruler", and say that for every one unit of time measured by row A the dominoes fall through two units of space measured by row B. Or we can choose row B as our clock and row A as our ruler, and say that for every one unit of time measured by row B the dominoes fall through one-half unit of space measured by row A. After the dominoes start falling we define "time", and that is the point. The "time" that we define is not a fundamental observable in our universe, only "space" (relative position) is. We could not observe "time" until we derived "time" from relative motion within the observable quantity we called "space" (which is different to "distance").
The idea that time does not "exist" as an independent quantity would seem to be quite speculative, except for one very interesting fact. We know that Einstein's theory of special relativity (SR) describes the universe using "time". However, special relativity is not the most fundamental theory, as we said, it is derived from Einstein's theory of general relativity (GR). The tools of special relativity give us less generalized solutions that are correct only under a limited set of circumstances. In general relativity the universe is described by solutions to Einstein's field equations. Most physicists believe that a particular description of the universe is correct only if it is a solution to those field equations. The amazing fact is that Einstein's field equations can be solved without any reference whatsoever to a temporal variable of any kind, indeed the field equations may be solved without even defining "time". This astounding fact greatly increases our confidence that we live in an essentially atemporal world.
A respected physicist named Carlo Rovelli has published what we find to be the best exposition of the lack of "time" in general relativity. A recent summary of his views is found in "Forget Time". In a preprint of a chapter he wrote for the book ,"Physics Meets Philosophy at the Planck Scale", Callender and Hugget eds., Cambridge University Press, Rovelli also summarizes the situation (the download is linked to a PDF file, the preprint is also available in other formats from http://xxx.lanl.gov/abs/gr-qc/9903045.) Rovelli's original work, published in the 1980's, is available as a pdf version of a LaTex file time.tex.pdf (some text was lost in converting the format). The paper goes into more detail about presymplectic mechanics and the Heisenberg view of quantum space-time. Acrobat PDF reader is available at http://www.adobe.com/support/downloads/acrwin.htm.) See also Carlo Rovelli's website.
In his technical explanation of the lack of a fundamental "time", Rovelli says: "In classical GR, a point in the physical phase space, or a state, is a solution of Einstein equations, up to active diffeomorphisms. A state represents a 'history' of space-time. The quantities that can be unequivocally predicted are the ones that are independents from the coordinates, namely that are invariant under diffeomorphisms. These quantities have vanishing Poisson brackets with all the constraints. Given a state, the value of each of these quantities is determined. In quantum gravity, a quantum state represents a 'history' of quantum space-time. The observables are represented by operators that commute with all the quantum constraints. If we know the quantum state of space-time, we can then compute the expectation value of any diffeomorphism invariant quantity, by taking the mean value of the corresponding operator. The observable quantities in quantum gravity are precisely the same as in classical GR."
"Some of these quantities may express the value of certain variables 'when and where' certain other quantities have certain given values... These quantities describe evolution in a way which is fully invariant under the parameter time, unphysical gauge evolution. The corresponding quantum operators are Heisenberg operators. There is no Schrodinger picture, because there is no unitary time evolution. There is no need to expect or to search for unitary time evolution in quantum gravity, because there is no time in which we should have unitary evolution. A prejudice hard to die wants that unitary evolution is required for the consistency of the probabilistic interpretation. This idea is wrong."
"In quantum gravity, I see no reason to expect a fundamental notion of time to play any role. But the nostalgia for time is hard to resist. For technical as well as for emotional reasons, many approaches to quantum gravity go out of their way to reinsert in the theory what GR is teaching us we should abandon: a preferred time. The time 'along which' things happen is a notion which makes sense only for describing a limited regime of reality. This notion is meaningless already in the (gauge invariant) general relativistic classical dynamics of the gravitational field. At the fundamental level, we should, simply, forget time."
The immediate question is how can the state of the universe evolve if there is no time in which it can evolve? How can the dominoes fall if there is no time for the dominoes to fall? The answer is that state evolution can occur even where there is no time. All that is required is some mechanical action like that provided by presymplectic mechanics. Rovelli says: "Mechanics may be defined as the general theory of the evolution of physical systems in time. From this point of view, time is required for the very definition of the elementary mechanical concepts. For instance, the state of the system is defined at a given time. In such a conceptual framework, (t)ime is required. However, there exists an alternative starting point for mechanics. This is provided by presymplectic mechanics. This formulation does not require the absolute time for defining the basic concepts of the theory. We shall illustrate presymplectic mechanics by first showing that Hamiltonian mechanics admits a reformulation in terms of a presymplectic space, and then noticing that this reformulation does not require the variable that represents time to be specified, or even defined. ... In presymplectic mechanics, which is an elegant generalization of standard hamiltonian mechanics, a dynamical system is just defined by a presymplectic manifold......"
After years of reading in this area, our intuitive feeling is that we do in fact live in an essentially atemporal universe, a world without a fundamental "time". However, we do not want to minimize the complexity of the issue. Most string theorists and quantum researchers believe that relativity is wrong, or at least incomplete, and that a fundamental "time" does exist. They take a radically different approach to the search for "quantum gravity" and "quantum space-time". Three excellent articles about the fascinating search for Quantum Gravity are included for your information (each PDF file may take several minutes to download on a dial-up connection): Prima Facie Questions in Quantum Gravity and Strings, loops and others: a critical survey of the present approaches to quantum gravity; plus an article about time and wave function collapse: Can we compute the exact time a quantum measurement happens? Also, here is an article that argues that none of this really matters: A possible solution to the problem of time in quantum cosmology.
Minkowski, who along with Einstein formalized the math of space-time, said, "…henceforth, space by itself, and time by itself, have vanished into the merest shadows and only a kind of blend of the two exists in its own right." The classic text on relativity by Wheeler and Taylor says about space and time "Equal footing, yes; same nature, no. There is a minus sign in this formula that no sleight of hand can ever conjure away. This minus sign marks the difference in character between space and time..." There are many, many physicists who believe that space-time has a radically different nature than we think it does. However, despite the absence of a fundamental "time" in GR, few are willing to conclude that we live in some kind of a "spatial" universe that lacks any form of temporality. Many who agree that the universe lacks a fundamental temporal variable (t), still believe that the universe exhibits fundamental "temporality". They may be right. None-the-less, we strongly believe that we should accept what general relativity is telling us, and that we should look for an essentially spatial (relative position) model of our universe that will accommodate quantum mechanics.
Rovelli notes that: "Conventional field theories are not invariant under a diffeomorphism acting on the dynamical fields. (Every field theory, suitably formulated, is trivially invariant under a diffeomorphism acting on everything.) General relativity, on the contrary, is invariant under such transformations. More precisely, every general relativistic theory has this property. Thus, diffeomorphism invariance is not a feature of just the gravitational field: It is a feature of physics, once the existence of relativistic gravity is taken into account. Thus, one can say that the gravitational field is not particularly ``special'' in this regard, but that diff-invariance is a property of the physical world that can be disregarded only in the approximation in which the dynamics of gravity is neglected. What is this property? What is the physical meaning of diffeomorphism invariance?"
"Diffeomorphism invariance is the technical implementation of a physical idea, due to Einstein. The idea is a deep modification of the pre-general-relativistic (pre-GR) notions of space and time. In pre-GR physics, we assume that physical objects can be localized in space and time with respect to a fixed non-dynamical background structure. Operationally, this background spacetime can be defined by means of physical reference-system objects, but these objects are considered as dynamically decoupled from the physical system that one studies. This conceptual structure fails in a relativistic gravitational regime. In general relativistic physics, the physical objects are localized in space and time only with respect to each other. Therefore if we "displace"' all dynamical objects in spacetime at once, we are not generating a different state, but an equivalent mathematical description of the same physical state. Hence, diffeomorphism invariance"
"Accordingly, a physical state in GR is not 'located' somewhere (unless an appropriate gauge fixing is made). Pictorially, GR is not physics over a stage, it is the dynamical theory of (or including) the stage itself."
The following is VERY speculative, based mostly on intuition and not objective science, is offered for discussion only, and should not be considered in any way as actual theory. If you are interested in the current science of space-time, you can stop reading here.
We will now offer a few suggestions about what an atemporal model might look like, but before doing that we need to answer the question, so what? Why does it matter if time exists as a fundamental observable, or just as a derived quantity? The answer is that lack of a fundamental time may mean that we live in an essentially "spatial" (relative position) universe that may be profoundly different from the currently spatio-temporal model.
The Stanford Encyclopedia of Philosophy describes space-time as follows: "Virtually all modern space-time theories are now built in the same way. The theory posits a manifold of events and then assigns further structures to those events to represent the content of space-time."... "Consider our universe, which relativistic cosmologies attempt to model. Events in the universe correspond to the dimensionless points of familiar spatial geometry. Just as a geometric point is a particular spot in a geometrical space, an event is a particular point in a cosmological space at a particular time." (emphasis added)
If we live in an essentially spatial world, this universal model of space-time is probably wrong. In current temporal theories each point in space-time is associated with one sequential event, and one event only. If we live in an atemporal universe, each point in space-"time" may have multiple events associated with it. This is admittedly very speculative, but it is far too fascinating not to explore. We know from relativistic and quantum field theories that "objects" are in some sense waves that travel through space. If the universe is a four (or other number) dimensional "space", rather than a four dimensional "space-time", then waves may move through some kind of homogeneous "space", not "space-time".
The following diagram is intended to do no more than suggest the truly profound possibilities that an atemporal model may present. We have replaced the axis normally labeled t for time with an arbitrary w axis to reflect the fact that all four dimensions are identical in nature. All directions lead into "space", none into "time". We then arbitrarily suppress any two of the axis, and show the two remaining axis on the graph. We pick a point that is one unit out on the horizontal axis. Each graph represents state evolution due to presymplectic mechanics, visualizing sequential motion through an atemporal 4D space. The important thing to note is that a given point 1 unit out on the horizontal axis, can have associated with it multiple values in the other three dimensions.
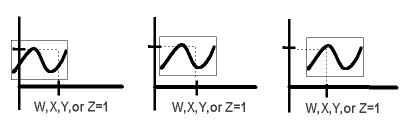
The whole point of this absurdly simplistic graph is to emphasize the possibility that in an atemporal universe every point in space can have multiple values as the wave "passes" through the space occupied by that point. Each value is an "event" at that point, each point represents multiple events. This cannot happen in a temporal model, simply because an event is a particular point in a cosmological space at a particular time. In a temporal universe if we observe a wave at a point in space-time it must have a particular value. In a world without temporality, if we observe a wave at a point in space-time it will have different values depending on the spatial order in which we observe the points.
We hesitate to mention this (it is extremely speculative and is offered to stimulate thought on the matter), but there is an intuitive commonsense feeling that the occurrence of the various possible values at each point in a truly spatial universe looks a lot like quantum probabilities. Indeed, we see that what determines the value that we observe at a given point in a spatial universe is the physical observation itself. In other words, in our simplistic graph above, if we look at the first frame we see a particular value, if we look at the second frame we see another value, if we look at the third frame we see a third value, etc. This "feels" a lot like the Copenhagen interpretation where observation determines the value when the "wave function collapses".
Indeed, there are similarities to the virtually ignored, yet very interesting, "transactional interpretation" of quantum mechanics proposed some ten years ago by the physicist John Cramer, who said: "To summarize the transaction model, the emitter produces a retarded offer wave (OW) which travels to the absorber, causing the absorber to produce an advanced confirmation wave (CW) which travels back down the track of the OW to the emitter. There the amplitude is CW1~|OW2|2, where CW1 is evaluated at the emitter locus and OW2 is evaluated at the absorber locus. The exchange then cyclically repeats until the net exchange of energy and other conserved quantities satisfies the quantum boundary conditions of the system, at which point the transaction is complete. Of course the pseudo-time sequence of the above discussion is only a semantic convenience for describing the onset of the transaction. An observer, as in the simpler plane wave case, would perceive only the completed transaction which he could reinterpret at the passage of a single retarded (i.e., positive energy) photon traveling at the speed of light from emitter to absorber."
"But an equally valid interpretation of the process is that a four-vector standing wave has been established between emitter and absorber. As a familiar 3-space standing wave is a superposition of waves traveling to the right and left, this four-vector standing wave is the superposition of advanced and retarded components. It has been established between the terminating boundaries of the emitter, which blocks passage of the advanced wave further down the time stream, and the absorber, which blocks passage of the retarded wave further up the time stream. This space-time standing wave is the transaction..."
The general idea is that there may be an interaction between advanced and retarded waves in space-time that provides a mechanism whereby what is commonly called the future interacts with what is called the past and present. If we live in an atemporal universe, we would simply say that the transactional interpretation might offer the possibility of a dynamic interaction between points in space-time, so that the space-time events themselves have a dynamic nature that is not recognized in current theory.
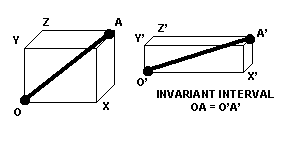
If the time and space dimensions are identical in nature, we would need to rethink what the minus sign means in the formula for the invariant interval: ds^2 = dx^2 + dy^2 + dz^2 - dt^2. The value of the invariant interval is invariant under Lorenz transformations. Perhaps the minus sign should be thought of as a limitation on the relative spatial separation (change in relative position or values for sets of relative position) of objects, rather than as a manifestation of temporality.
By now you may be familiar with the lightcone. It gives us a good visualization of the geometry of light traveling into space-time, however you should realize that it is a diagram that is drawn by suppressing a spatial dimension. In fact, light propagating outward from a point in space-time maps a four dimensional solid sphere (that can be thought of as an infinite series of ever larger nested spheres).
Think about an explosion at a single point in space-time. We would argue that photons stream outward in all directions, propagating in all 4 dimensions (for a better description, see page 194 of the popular text, The Emperor's New Mind, by Roger Penrose). As the photons fly outward they map a 4D solid sphere. The area inside the sphere is inside the light-cone, the area outside the sphere is outside the light-cone, and the surface of the sphere is the surface of the light-cone. The inside area of the sphere, essentially the solid part of the sphere, represents what we consider to be the derived "temporality" of our universe.
If our invariant interval OA represents the path of a photon, it can be visualized as the radius of the "light-sphere" as it expands into space-time. If so, the points x, y, and z are inside the sphere, and are therefore inside the light-cone. We can do an invariant transformation from x, y, z to x', y', z'. Any such transformation yields points within the light-sphere. It seems intuitively true that the minus sign tells us that the relative spatial separation of all points (and any events/objects at those points) is dictated by the value of the invariant interval. We would interpret the minus sign as the geometric reality that events/objects that are time-like separated must fall within the light-sphere. This conclusion has nothing to do with temporality, and everything to do with spherical geometry.
Cramer makes no claims that the transactional interpretation is anything more than an interpretation of the existing formalism of quantum mechanics. Nor does he suggest that the universe is atemporal. Yet there is an intuitive feeling that if we do live in a universe that lacks fundamental temporality, the transactional approach might provide answers to some of the most difficult questions in quantum physics and relativity. If advanced and retarded waves repeatedly pass through the same point in space-time, then probability would determine what an observer saw at that point, and quantum entanglement might be explained.
We believe that acceptance of the absence of fundamental temporality, along with a deeper understanding of the difference between distance and relative spatial separation (between discrete events as explained by causal set theory), will provide a key to understanding the physical relationship between quantum mechanics and relativity . This is as good a "time" as any to clearly state that we realize that human beings will never abandon, nor do they need to abandon, references to the "time" we derive from relative motion. It is perfectly valid to define sequential events that evolve due to presymplectic mechanics, or any other atemporal process, as "time". Yet doing so does not change our belief that until we derive "time", there is no fundamental "time" in the universe. It seems wrong to say that the fact that tomorrow will arrive proves that "time" exists. It is not wrong to label as "tomorrow" the sequence of events that, due to atemporal state evolution, "follows" the sequence of events that we define as "today".
It is not wrong to say that the sun rises and the sun sets, yet it seems wrong to say that because the sun rises and sets a "fundamental temporal order" exists. We may live in some kind of "block universe", however its dimensiaonal structure may be more complex than time and space. No matter what details we may eventually discover about our universe, I believe that the universe we live in is fully relativistic and fundamentally atemporal. As Rovelli says in "A note on the foundation of relativistic mechanics. II: Covariant hamiltonian general relativity to field theory" (http://xxx.lanl.gov/abs/gr-qc/0202079): "In this paper I have applied the ideas of (Relativistic observables and relativistic states, http://xxx.lanl.gov/abs/gr-qc/0111037). I have argued that the relativistic notions of state and observable lead naturally to the formulation of field theory over a finite dimensional space. The application of this formulation to general relativity leads to a remarkably simple hamiltonian formulation, in which the physical irrelevance of the spacetime coordinates becomes manifest...." "The form ... codes the dynamics as well as the symplectic structure of the theory."
If this is correct, we may live in a universe where physical systems exist in an atemporal configuration space. A configuration space that might be thought of somewhat like a "now" where physical "events" we currently view as being in the past or future of the system interact with each other. A fully relativistic universe where time and distance are meaningless, and where shape and relative spatial separation define the configuration space.
A brief additional comment on "distance". Return to our previous example of a universe with one, two, or three objects. Assume a universe containing two objects only. What is the distance between them? We cannot know what the distance is, simply because there is no ruler or other instrument to measure "distance". If we have objects at points A, B, & C, we can say that the distance from A to B is two units of the distance from B to C, or we can say that the distance from B to C is 1/2 the unit of distance from A to B. However, if we don't have an object at a point C, we can say nothing about the distance from A to B! Just as there is no time when objects do not move in the universe, there may be no distance when there are only two objects in the universe. Unless there is a third object to use as a ruler it may be that we cannot say what the "distance" is that separates objects. Perhaps the argument presented for an atemporal description of the universe can be equally applied to posit a universe where there is no fundamental "space". We intuitively conclude that there is no "distance" between objects, only relative "separation" resulting from relative "position".
This may seem strange, yet if we are successful in suppressing the human assumptions of temporality and distance, we can imagine a universe where physical reality has physical meaning only for those physical objects that engage in a relativistic ballet of existence. Perhaps if the objects are part of physical, atemporal, fully relativistic, interaction, they have a physical existence. Perhaps if the objects are not part of physical, atemporal, fully relativistic, interaction, they do not have a physical existence. While objects may have a non-physical existence, in an atemporal universe there is no physical meaning to the statements that objects that do not have a physical existence "did have a physical existence", or that they "will have a physical existence".
For a more recent discussion of why our point of view may be wrong, please see Petkov, Relativity, Dimensionality, and Existence, or may be right, please see Savitt, Chronogeometrical Determinism and the Local Present. Also please read the excellent article in the Stanford Encyclopedia of Philosophy on Being and Becoming in Modern Physics.
I would like to mention another very similar, very speculative, idea. In philosophy there is a lively discussion going on about what it means to “become” and to “be”. In physics there is a general consensus that Spacetime does not allow for such a distinction, that all events in Spacetime represent physical reality. Given the progress in understanding what GR is telling us, I believe that the view of Spacetime as representing physical reality is not necessarily correct.
If there is no fundamental temporal variable in GR, and we therefore live in an essentially atemporal universe, we need to rethink the implications for our physical existence. For example, visualize a human being placed in a particular spot in three dimensional space, something we are very familiar with. Now open your mind to the possibility that the human being actually occupies an "area" in four essentially spatial dimensions. A human being is more than a static object, so they must necessarily occupy more than a single, frozen, point in spacetime. It is very difficult to visualize a human being as what is essentially a sequentially evolving event in spacetime, because our brains are wired to view ourselves as living in one moment in time, not as a system occupying a defined area of 4D Spacetime.
It might help if you visualize the person having a thought like “I will walk the dog”. We naturally think of all thoughts as being instantaneous, yet I would argue that any thought not only occurs at a place in three dimensions, but also occupies a tiny bit of area in the fourth dimension. The mind (system) that creates the thought “I will walk the dog” not only occupies an area in 3D space, it also occupies a discrete area of the fourth dimension because the components of the thought are necessarily sequentially evolving. In other words, in an atemporal universe the physical structure of the thought “I will walk the dog” is four dimensional, not three dimensional.
You might be wondering if a system that creates a thought like “I will walk the dog” occupies an area of 4D space, how do we know where the boundaries of that thought are? Should we include more of the thought like “I will walk the dog before I go to work”? Is our idea that a thought occupies 4D simply an arbitrary, abstract, concept? We often talk about the worldline of particles, and the worldline of human beings, as if both are identical concepts. That loose understanding is acceptable as long as we are able to localize our concept of human existence to a single point on a worldline, but if we live in a fundamentally atemporal universe we must view the physical reality of a human being not as a point, but rather as occupying a segment of a worldline. How long should that segment be?
The physical existence of a human being is a complex system of interrelated, yet also independent, particles. It seems that the question when we ask about the thought “I will walk the dog” should be which component “particles” do we include as part of the “human system” having that thought? That is rather like asking where does a river end? We know that a river ends when we are in the ocean, and when we are on dry land, however there is a gray area in the delta and along the shore where we will differ when asked is that part of the river? In an atemporal 4D space we may differ as to what particles belong to a particular “human system”, much as we might argue in 3D whether a hair cut from our head is still part of our body, yet that does not mean that we cannot easily identify the 4D human being who has the thought.
What are the physical consequences of our view? We can reach some agreement on what discrete area of 4D Spacetime a person occupies. But let’s simplify things further. Assume that a particle that is part of the human being exists (i.e.- the worldline of that particle is increasing in length). Without even defining time, we can say for a fact that there is a set of particles that have a relationship with that particle. An aside, relativity is all about relationships. In a universe totally devoid of any objects relativity is meaningless. In our universe, everything in general relativity is based on the relationship of objects. Therefore, our particle has a relativistic relationship with only those objects (particles) that have physical existence, reality, in our universe.
My incredibly speculative suggestion is that in an atemporal universe for every physical object there is a fundamental distinction between all objects that have physical existence (represented by worldlines that in some sense are 'expanding', growing longer) and “objects” that do not have physical existence (represented by worldlines that in a similar sense have a 'fixed length'). For each particle there are a set of particles with which that particle has a relativistic relationship, the set of all such particles is that which is physically real for that particle.
There is an immediate objection that GR requires that all points in Spacetime have physical existence, but this is not true. We have imposed an interpretation on the math of GR that says that Spacetime represents physical reality, yet as far as I can tell, an interpretation that declares a limited region of Spacetime to be physically real is fully consistent with GR, does nothing to the math of Spacetime outside that area (which in a sense becomes a boundary condition), and is not prohibited by quantum theory? It is much like the Transactional Interpretation of QM by John Cramer, which is an alternate interpretation to the Copenhagen Interpretation and that is fully consistent with the math of quantum theory. I may be wrong, yet saying that for a particular particle there is a discrete area of Spacetime that represents physical reality, and that all outside that area is outside the physical universe for that particle, is an interpretation that at least on the surface seems to me to be consistent with GR? (If you are bothered in any way by the possible nihilistic consequences if this is true, then please follow this link to read our books on the science and philosophy behind nihilism.)
The only sense that I can make of all of this is that it is necessarily true that there is a set of space-time events that exist in the past and future light-cone of an event that exists at a worldpoint, and there is a set of space-time events that do not exist in the past and future light-cone of an event that exists at a worldpoint. A composite object, anything more than a single particle, be it a human being or a tree, Does Not Exist, Exists, Does Not Exist. This is a radical idea that should be carefully considered before accepting, or rejecting.
In coming out of the dark ages human beings have made enormous intellectual leaps in philosophy and science, so much so that many now believe we understand how the universe works. We need to recognize the fact that when future generations look back at twenty-first century science it will seem as primitive to them as alchemy does to us, and they will be rightly amazed at our lack of understanding of our existence. Indeed there are glimpses of a possible future that might provide a solid theoretical foundation for existential consciousness, which would give meaning to our lives in ways that we cannot yet imagine. In our other publications.) we argue that existence of a non-physical soul is a far more rational belief than trying to find existential meaning in a humanistic, physical, model. We don't know where science will take us, so once again we must caution that our conclusions may be wrong.
last major rev. 4/4/01, minor rev. 2025 Send comments to: spacetime@ws5.com
SpaceTime is Sponsored by our philosophy and religion sites. Please visit our sites by clicking below:
This Website Copyright Compact Library Publishers Inc. 1998 - 2014 all rights reserved